Small Group Tuition

Provide your child with stable and consistent support in maths to compliment their school learning, by signing them up for our Online Group Tuition programme.

We all want to give our children the best oportunities in life, but in the fast paced environment we live in, it can seem impossible to fit everything in.

With our online tutoring programme, you can offer your child a chance to:

  • Take control of their learning

  • Consolidate and grow their maths knowledge

  • Build their confidence, and

  • Bring a sense of structure into their extra-curricular learning routine

…Without taking on the extra workload yourself!

online learning 6
group learning zoom
Capture2
online learning 5
indep learning comp ethnic
boys laptop
online learning 7
online learning 8
Join The Waiting List For The Next Round Of Small Group Tuition

How does the Online Group Tuition Programme work?

We run two rounds of online tuition in an academic year, that each run for 21 weeks.

Round 1 starts in September, and Round 2 starts in January.

A different topic is taught each week for 21 weeks, covering 3 grades worth of content, either:

Grade 1 – 3

Grade 4 – 6, or

Grade 7 – 9

You can view a breakdown of the topics we cover at the bottom of this page. Depending on your child’s current grade, and after discussion with you, we would recommend and enroll them on to the class that is the best pitch for them to make maximum progress in the 21 weeks.

What happens after the 21 week course is complete?

This is ultimately up to you and your child!

If your child loved the online programme (and we’re sure they will) and excelled in their learning during round 1, they can be enrolled for round 2 in to the higher grade programme to continue to grow and nurture their passion for maths!

Alternatively, if you decide you would like your child to have bespoke, individualised support, you can explore our one to one tuition options.

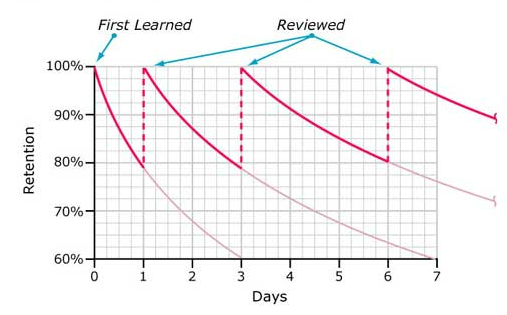
And if they found round 1 helpful, but feel like they could benefit from looking at the content again, they are absolutely welcome to – research has shown that the more times children are exposed to a topic or concept, the longer they remember the knowledge for each time.

This graph demonstrates that students remember information for longer, the more times they are exposed to it. This is why frequent review of knowledge is key to committing mathematical concepts to our long term memory. Image by Wellington Learning And Research Centre.

Case Study

Cameron and Joshua are brothers with an age gap of two years. When their parents came to us, Cameron was in his first year at secondary school but was struggling with the transition and appeared to be falling behind his peers, while Joshua was thriving in year 5 and expecting to do very well in his SATs. Although different in age, after a discussion with their parents, we decided to enroll them on to the same small group learning programme, Grade 1 - 3. This gave Cameron a chance to recap and revise many of the basic fundamental maths topics and consolidate his prior learning, to put him in a stronger position to keep up at school. Meanwhile, Joshua benefitted from being stretched and challenged beyond the primary curriculum to feed his passion for maths and introduce him to new and exciting topics that will prepare him for future learning. In addition, because they were in the same class, they could collaborate and help each other - both inside and outside of the programme - as well as learn from others in the class. As a result of this approach, Cameron was able to catch up with his peers at school during the course of the 21 weeks and no longer required our support, while Joshua decided to take up private tuition to help him work towards a specific goal - the 11+ exams!
Cameron and Joshua B
Year 7 and Year 5

Maths Topics Covered In The Small Group Learning Programme

Grade 1 - 3

Grade 4 - 6

Grade 7 - 9

  1. Place value
  2. Ordering decimals
  3. Writing algebraic expressions
  4. Congruent shapes
  5. Types of angles
  6. Probability scales
  7. Pictograms
  8. Adding and subtracting decimals
  9. Money problems
  10. Factors, multiples and primes
  11. Rounding to decimal places
  12. Collecting like terms
  13. Multiplying terms
  14. Area of a rectangle
  15. Multiplying decimals
  16. Adding and subtracting fractions
  17. Finding a fraction of an amount
  18. Expanding single brackets
  19. Factorising
  20. Sharing in a given ratio
  21. Surface area of cuboids
  1. Laws of indices
  2. Expanding double brackets
  3. Solving equations
  4. Rearranging
  5. Similar shapes
  6. Pythagoras
  7. Tree diagrams
  8. Negative indices
  9. Factorsing and solving quadratics
  10. The difference of two squares
  11. Compound interest and depreciation
  12. Area and sectors of a circle
  13. Trigonometry
  14. Harder tree diagrams 
  15. Recurring decimals to fractions
  16. Expanding triple brackets
  17. Iteration
  18. Transformations
  19. Circle theorems
  20. Cumulative frequency
  21. Box plots
  1. Fractional indices
  2. Rearranging equations
  3. Solving quadratics with the formula
  4. Direct proportion
  5. The sine rule
  6. The cosine rule
  7. Using ‘and’ / ‘or’ rules in probability
  8. Surds – simplifying
  9. Surds – manipulating
  10. Surds – rationalising
  11. Completing the square – factorising
  12. Completing the square – solving
  13. Algebraic fractions – simplifying
  14. Algebraic fractions – solving
  15. Simulataneous equations
  16. Quadratic simultaneous equations
  17. Solving inequalities
  18. Solving quadratic inequalities
  19. Similar shapes – area and volume
  20. Pythagoras in 3D
  21. Tirgonometry in 3D
Take a look at our 7 Steps To Success Videos